Gli integrali sono uno dei concetti fondamentali della matematica, strettamente legati al calcolo differenziale e integrale. In termini semplici, un integrale rappresenta un’operazione che consente di calcolare l’area sottesa a una curva in un intervallo specifico o di sommare infinitamente piccole quantità.
Tipi di Integrali
- Integrale Indefinito: Rappresenta una famiglia di funzioni primitive di una data funzione. È scritto come:
∫f(x) dx=F(x)+C∫f(x)dx=F(x)+C
dove F(x)F(x) è una primitiva di f(x)f(x) e CC è una costante arbitraria.
- Integrale Definito: Calcola l’area sotto la curva di una funzione tra due punti aa e bb. È espresso come:
∫abf(x) dx=F(b)−F(a)∫abf(x)dx=F(b)−F(a)
dove FF è una primitiva di ff. Questo integrale fornisce un valore numerico che rappresenta l’area compresa tra il grafico della funzione, l’asse xx e le linee verticali x=ax=a e x=bx=b .
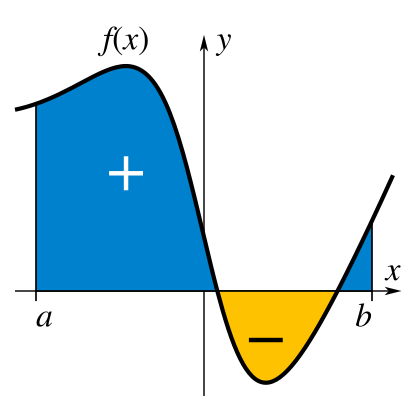
Interpretazione Geometrica
Geometricamente, l’integrale definito può essere interpretato come l’area “orientata” sottesa dalla curva. Se la funzione assume valori negativi, l’area corrispondente viene considerata negativa, mentre le aree sopra l’asse xx sono positive. Questo concetto è essenziale per comprendere come gli integrali possano essere utilizzati per calcolare aree, volumi e altre grandezze fisiche.
Teorema Fondamentale del Calcolo
Il teorema fondamentale del calcolo stabilisce un collegamento tra derivazione e integrazione, affermando che l’integrazione è l’operazione inversa della derivazione. Esso afferma che se FF è una funzione continua su un intervallo chiuso [a,b][a,b] e ff è la sua derivata, allora:
∫abf(x) dx=F(b)−F(a)∫abf(x)dx=F(b)−F(a)
Questo teorema consente di calcolare integrali definiti utilizzando le primitive, semplificando notevolmente il processo di integrazione .
Applicazioni degli Integrali
Gli integrali hanno numerose applicazioni in vari campi, tra cui:
- Fisica: Calcolo di lavoro, energia, e altre grandezze fisiche.
- Ingegneria: Analisi di strutture e sistemi dinamici.
- Economia: Determinazione di costi e ricavi totali.
- Statistica: Calcolo di probabilità e distribuzioni.
Conclusione
In sintesi, gli integrali sono uno strumento matematico fondamentale che permette di calcolare aree, volumi e altre grandezze attraverso l’analisi delle funzioni. La loro comprensione è cruciale per avanzare nello studio del calcolo e delle sue applicazioni in vari ambiti scientifici e ingegneristici.
Sebbene gli integrali siano uno strumento matematico fondamentale con numerose applicazioni scientifiche, la loro utilizzo pratico nella vita quotidiana è piuttosto limitato per la maggior parte delle persone. Ecco alcuni esempi di come gli integrali possono essere applicati in contesti pratici:
Calcolo del Consumo di Carburante
Gli integrali possono essere utilizzati per calcolare la quantità di carburante bruciata da un’auto in movimento. Integrando la portata di carburante rispetto al tempo o alla distanza percorsa, si può determinare il consumo totale.
Calcolo del Tempo di Viaggio
Conoscendo la velocità di un veicolo in funzione del tempo o della distanza, è possibile utilizzare gli integrali per calcolare il tempo totale di un viaggio. Integrando l’inverso della velocità rispetto alla distanza si ottiene il tempo.
Calcolo di Aree e Volumi
Gli integrali definiti permettono di calcolare aree sottese da curve e volumi di solidi di rotazione. Sebbene non siano applicazioni quotidiane, queste tecniche trovano utilizzo in progettazione e ingegneria.
Calcolo di Probabilità
In statistica, gli integrali sono utilizzati per calcolare probabilità e distribuire variabili continue. Ad esempio, integrando una funzione di densità di probabilità su un intervallo si ottiene la probabilità che una variabile casuale cada in quell’intervallo. In generale, gli integrali sono uno strumento matematico potente con molteplici applicazioni scientifiche, ma il loro utilizzo pratico nella vita di tutti i giorni è limitato per la maggior parte delle persone. Tuttavia, la capacità di comprendere e applicare i concetti di integrazione rimane importante per chi studia matematica e scienze.