Le derivate in matematica sono uno strumento fondamentale del calcolo differenziale, utilizzato per studiare il comportamento e le proprietà di funzioni. In particolare, la derivata di una funzione in un punto rappresenta la velocità di variazione della funzione in quel punto.

Definizione di derivata

Sia f una funzione definita in un intervallo che contiene il punto x. La derivata di f in x, indicata con f'(x), è definita come:

f′(x)=lim_h→0​ f(x+h)−f(x)/h

​Questa espressione rappresenta il limite del rapporto incrementale (o rapporto delle differenze) quando l’incremento h tende a zero.

Interpretazione geometrica

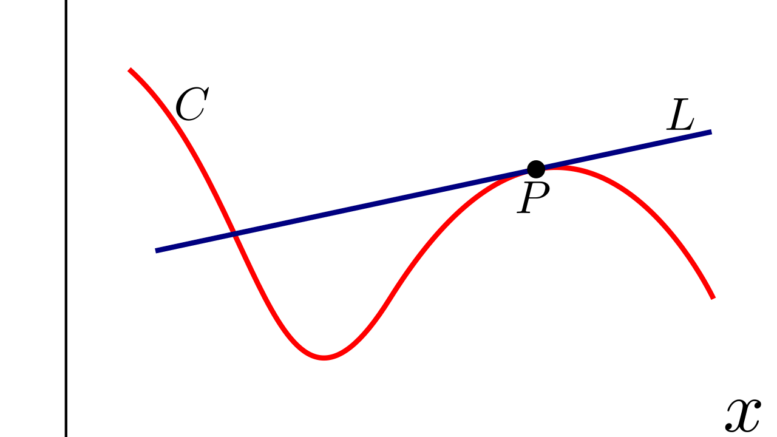
Geometricamente, la derivata di una funzione in un punto rappresenta la pendenza della retta tangente al grafico della funzione in quel punto. Questa retta tangente è la migliore approssimazione lineare della funzione nell’intorno del punto considerato.

Regole di derivazione

Esistono diverse regole che permettono di calcolare le derivate di funzioni elementari e di combinazioni di funzioni. Alcune delle principali regole sono:

1. Derivata della costante: se f(x) = c, allora f'(x) = 0
2. Derivata della potenza: se f(x) = x^n, allora f'(x) = nx^(n-1)
3. Derivata della somma: se f(x) = g(x) + h(x), allora f'(x) = g'(x) + h'(x)
4. Derivata del prodotto: se f(x) = g(x)h(x), allora f'(x) = g'(x)h(x) + g(x)h'(x)
5. Derivata del quoziente: se f(x) = g(x)/h(x), allora f'(x) = (g'(x)h(x) – g(x)h'(x))/(h(x))^2

Applicazioni delle derivate

Le derivate trovano applicazione in numerosi ambiti della matematica e della fisica, tra cui:

• Studio del comportamento di funzioni (punti stazionari, massimi e minimi, concavità)
• Velocità e accelerazione in cinematica
• Ottimizzazione di funzioni in problemi di massimo e minimo
• Approssimazione lineare di funzioni
• Calcolo di integrali (tramite il teorema fondamentale del calcolo integrale)

Le derivate sono uno strumento potente e versatile del calcolo differenziale, che permette di studiare il comportamento locale di funzioni e di applicare questo studio a numerosi problemi pratici e teorici. La comprensione delle derivate è fondamentale per proseguire nello studio dell’analisi matematica e delle sue applicazioni.