di Sergio Mauri

Il monomio è un’espressione matematica che consiste in un prodotto di fattori qualsiasi, siano essi numerici o letterali. I fattori letterali hanno per esponente un numero naturale. Es:

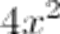
Il fattore numerico 4 prende il nome di coefficiente, mentre il fattore letterale (x²) costituisce la parte letterale.

La definizione di monomio presenta 3 diversi ingredienti:

1. la parte numerica può essere costituita da un qualsiasi numero;
2. la parte numerica deve essere moltiplicata per la parte letterale;
3. nella parte letterale possono esserci solamente moltiplicazioni

Da notare che le potenze sono particolari moltiplicazioni in cui i fattori coincidono con la base, rientrano perciò nella regola della definizione. Es:

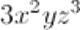
è un monomio in cui 3 è il coefficiente numerico, mentre x²yz³ è la parte letterale

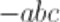
è un monomio che ha per coefficiente numerico -1 (che è un numero relativo, cioè un numero intero caratterizzato da un segno positivo, negativo o nullo) mentre abc è la parte letterale.

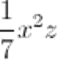
È un monomio con coefficiente numerico 1/7 (numero razionale, cioè un numero che può essere espresso sotto forma di frazione con numeratore e denominatore dati da numeri interi), mentre la parte letterale è x²z.

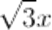
È un monomio con parte numerica

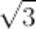
(numero irrazionale, cioè un numero decimale illimitato non periodico che quindi non può essere espresso sotto forma di frazione), mentre la parte letterale è x.

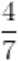
è un monomio con una qualsiasi lettera con esponente zero, che perciò vale 1. Il coefficiente è

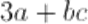
non è un monomio, perché l’espressione non si può scrivere come prodotto tra una parte numerica e una parte letterale.

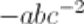
Non è un monomio, perché l’esponente della lettera C è negativo.

Non è un monomio, poiché attraverso la definizione di “potenza con esponente negativo” possiamo riscriverlo nella forma

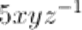
da cui si vede che l’esponente di z è negativo e quindi non è un numero naturale.

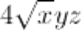
Non è un monomio perché equivale a

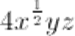
e l’esponente di x non è intero (positivo).