La teoria degli insiemi è un ramo fondamentale della matematica che si occupa dello studio degli insiemi, ovvero collezioni di oggetti che possono essere numerici, logici o concettuali. Questa teoria è alla base di molte altre discipline matematiche e ha avuto un grande sviluppo a partire dalla seconda metà del XIX secolo grazie al lavoro di matematici come Georg Cantor, Ernst Zermelo e Adolf Fraenkel.
Fondamenti della Teoria degli Insiemi
- Definizione di Insieme: un insieme è una collezione di oggetti distinti, chiamati elementi. Gli insiemi possono essere definiti in vari modi, ad esempio per elencazione (come {1, 2, 3}) o tramite una proprietà che caratterizza i loro elementi.
- Notazione: gli insiemi sono solitamente rappresentati con lettere maiuscole (es. A, B, C) e gli elementi con lettere minuscole (es. a, b, c). Si usa il simbolo ∈ per indicare che un elemento appartiene a un insieme (es. a∈Aa∈A).
- Operazioni tra Insiemi:
- Unione: l’unione di due insiemi A e B, denotata A∪BA∪B, è l’insieme che contiene tutti gli elementi che appartengono a almeno uno dei due insiemi.
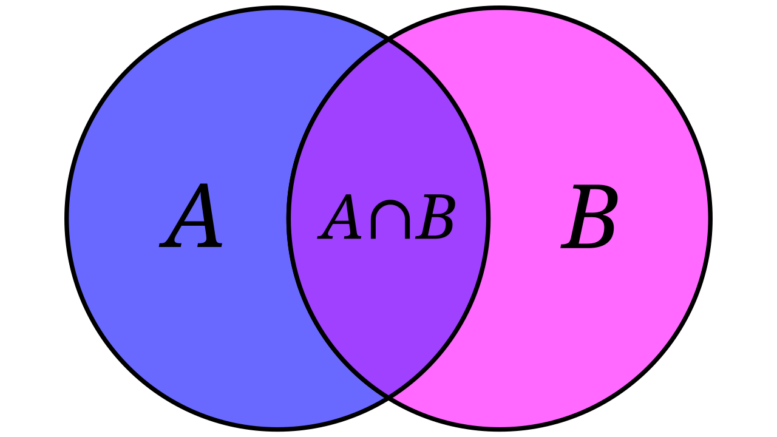
- Intersezione: l’intersezione di A e B, denotata A∩BA∩B, è l’insieme degli elementi che appartengono sia a A che a B.
- Differenza: la differenza tra A e B, denotata A∖BA∖B, è l’insieme degli elementi che appartengono a A, ma non a B.
- Complemento: il complemento di un insieme A rispetto a un universo U è l’insieme degli elementi di U che non appartengono ad A.
- Cardinalità: la cardinalità di un insieme è il numero di elementi che contiene. Per esempio, se A={1,2,3}A={1,2,3}, allora la cardinalità di A, denotata |A|, è 3.
- Sottoinsiemi: un insieme B è un sottoinsieme di A se ogni elemento di B è anche un elemento di A, denotato come B⊆AB⊆A.
Importanza della Teoria degli Insiemi
La teoria degli insiemi è considerata il fondamento della matematica moderna, in quanto fornisce un linguaggio e una struttura per formulare concetti matematici in modo rigoroso. Essa è stata al centro di dibattiti sui fondamenti della matematica, specialmente nei primi decenni del XX secolo, e ha portato alla formulazione di assiomi, come il sistema assiomatico di Zermelo-Fraenkel.
Applicazioni
La teoria degli insiemi trova applicazione in vari campi:
- Algebra: per definire strutture algebriche come gruppi e anelli.
- Analisi: nello studio delle funzioni e delle loro proprietà.
- Logica: per formulare argomentazioni e ragionamenti matematici.
- Statistica: nella definizione di eventi e probabilità.
Per concludere la teoria degli insiemi è un pilastro della matematica che consente di organizzare e analizzare collezioni di oggetti in modo sistematico. La sua comprensione è essenziale per affrontare argomenti più complessi in matematica e nelle sue applicazioni pratiche.