di Sergio Mauri

L’algoritmo di PageRank è un algoritmo utilizzato da Google per classificare le pagine web in base alla loro importanza e autorevolezza. La formula di base per calcolare il PageRank di una pagina è la seguente:

PR(A)=(1−d) +d ( PR(T1​)​/ C (T1) + PR(T2​) / C(T2) + …. PR(Tn​)/ C(Tn))

dove:

• PR(A) rappresenta il PageRank della pagina A.
• PR(Ti​) rappresenta il PageRank delle pagine collegate a A (dove Ti​ è una pagina collegata ad A).
• C(Ti​) rappresenta il numero di link uscenti dalla pagina Ti​.
• d è il fattore di smorzamento, un valore compreso tra 0 e 1 che rappresenta la probabilità che un utente continui a seguire i link anziché saltare casualmente da una pagina all’altra. Solitamente, d è impostato intorno a 0.85.

La formula descrive il PageRank di una pagina come una combinazione ponderata tra il PageRank delle pagine che la collegano e il numero di link uscenti da ciascuna di queste pagine. Il fattore di smorzamento è introdotto per garantire che il PageRank sia distribuito in modo equo e per evitare cicli nel grafo delle pagine web.

L’algoritmo di PageRank viene eseguito iterativamente fino a quando i valori di PageRank convergono, cioè quando le differenze tra le iterazioni successive diventano trascurabili. Questo processo permette di ottenere una stima stabile e affidabile del PageRank per ciascuna pagina web nel web.

Quanto detto si collega con la Catena di Markov (Markov Chain). Una catena di Markov è un modello matematico che rappresenta una sequenza di eventi in cui la probabilità che un evento futuro dipende solo dallo stato attuale e non dai precedenti. In altre parole, una catena di Markov è un processo stocastico senza memoria, dove il futuro dipende solo dallo stato presente e non dalla storia passata.

Le principali caratteristiche di una catena di Markov includono:

1. Stati: una catena di Markov consiste in un insieme finito o infinito di stati. Ogni stato rappresenta una situazione o una condizione che può verificarsi nel sistema modellato dalla catena.
2. Matrice di transizione: la probabilità di transizione è rappresentata da una matrice, spesso chiamata matrice di transizione di Markov. Questa matrice indica le probabilità condizionate di passare da uno stato all’altro in un singolo passaggio.
3. Proprietà di Markov: la proprietà di Markov afferma che la probabilità di transizione da uno stato all’altro dipende solo dallo stato attuale e non dal percorso precedente attraverso gli stati.
4. Stato stazionario: in una catena di Markov, un vettore di probabilità è chiamato stazionario se rimane invariato quando moltiplicato per la matrice di transizione. Questo vettore rappresenta la distribuzione di probabilità degli stati nel lungo termine.

Le catene di Markov sono ampiamente utilizzate in vari campi, tra cui l’ingegneria, l’economia, la biologia, la fisica e l’informatica. Sono utili per modellare una vasta gamma di processi dinamici e sequenziali, come ad esempio:

• Processi decisionali sotto incertezza.
• Evoluzione di sistemi biologici e popolazioni.
• Comportamento di sistemi complessi come reti di computer e reti sociali.
• Analisi di sequenze di dati, come sequenze di DNA.
• Predizione del tempo e modelli climatici.

Le catene di Markov forniscono uno strumento potente per analizzare e comprendere il comportamento di sistemi dinamici e casuali, e le loro applicazioni si estendono a numerosi settori della scienza e dell’ingegneria.

La catena di Markov è strettamente collegata all’algoritmo di PageRank utilizzato da Google per classificare le pagine web nei risultati di ricerca. Ecco come si collegano:

1. Rappresentazione delle pagine web come stati: nell’algoritmo di PageRank, le pagine web sono rappresentate come stati della catena di Markov. Ogni pagina web corrisponde a uno stato all’interno della catena.
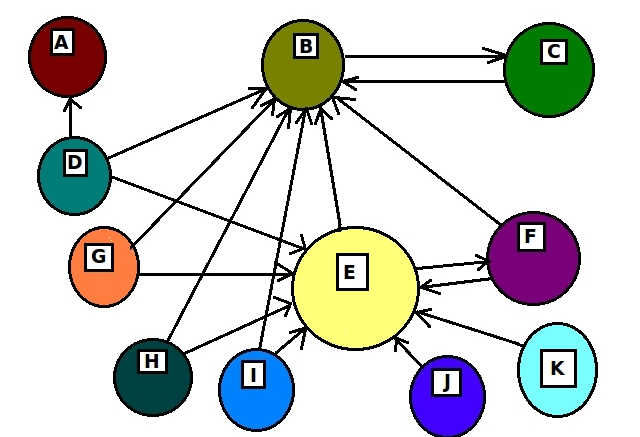
2. Transizioni tra le pagine: le transizioni tra le pagine web sono modellate dalle probabilità di transizione della catena di Markov. Se una pagina web A contiene un link che porta alla pagina web B, allora c’è una transizione dalla pagina A alla pagina B con una certa probabilità.
3. Importanza delle pagine: il PageRank di una pagina web è calcolato utilizzando il concetto di stazionarietà nella catena di Markov. Il PageRank di una pagina è proporzionale alla probabilità che un utente casuale termini nella pagina visitando casualmente le pagine web seguendo i link.
4. Matrice di transizione di Markov: la matrice di transizione di Markov viene costruita utilizzando i link tra le pagine web. Ogni riga della matrice rappresenta la probabilità di transizione da una pagina ad altre pagine, e la somma delle probabilità in ogni riga è uguale a 1.
5. Iterazioni per il PageRank: il calcolo del PageRank coinvolge iterazioni successive della catena di Markov fino a raggiungere un punto di convergenza. Durante ogni iterazione, vengono aggiornati i valori del PageRank in base alle probabilità di transizione tra le pagine web.

In sintesi, l’algoritmo di PageRank utilizza concetti fondamentali delle catene di Markov per valutare l’importanza e l’autorevolezza delle pagine web, aiutando così a determinare il loro posizionamento nei risultati di ricerca di Google. La teoria delle catene di Markov fornisce un quadro matematico potente per comprendere e analizzare il comportamento delle pagine web e dei link che le collegano.